python实现堆(最大堆、最小堆、最小最大堆) 当前观察
2023-04-03 14:31:55
来源:腾讯云
 (资料图)
(资料图)
1. 最大堆
class MaxHeap: def __init__(self): self.heap = [] def parent(self, i): return (i - 1) // 2 def left_child(self, i): return 2 * i + 1 def right_child(self, i): return 2 * i + 2 def get_max(self): if not self.heap: return None return self.heap[0] def insert(self, item): self.heap.append(item) self._heapify_up(len(self.heap) - 1) def extract_max(self): if not self.heap: return None max_item = self.heap[0] last_item = self.heap.pop() if self.heap: self.heap[0] = last_item self._heapify_down(0) return max_item def _heapify_up(self, i): while i > 0 and self.heap[i] > self.heap[self.parent(i)]: self.heap[i], self.heap[self.parent(i)] = self.heap[self.parent(i)], self.heap[i] i = self.parent(i) def _heapify_down(self, i): max_index = i left = self.left_child(i) if left < len(self.heap) and self.heap[left] > self.heap[max_index]: max_index = left right = self.right_child(i) if right < len(self.heap) and self.heap[right] > self.heap[max_index]: max_index = right if i != max_index: self.heap[i], self.heap[max_index] = self.heap[max_index], self.heap[i] self._heapify_down(max_index)if __name__ == "__main__": max_heap = MaxHeap() max_heap.insert(1) max_heap.insert(2) max_heap.insert(0) max_heap.insert(8) print(max_heap.get_max())2. 最小堆
class MinHeap: def __init__(self): self.heap = [] def parent(self, i): return (i - 1) // 2 def left_child(self, i): return 2 * i + 1 def right_child(self, i): return 2 * i + 2 def get_min(self): if not self.heap: return None return self.heap[0] def insert(self, item): self.heap.append(item) self._heapify_up(len(self.heap) - 1) def extract_min(self): if not self.heap: return None min_item = self.heap[0] last_item = self.heap.pop() if self.heap: self.heap[0] = last_item self._heapify_down(0) return min_item def _heapify_up(self, i): while i > 0 and self.heap[i] < self.heap[self.parent(i)]: self.heap[i], self.heap[self.parent(i)] = self.heap[self.parent(i)], self.heap[i] i = self.parent(i) def _heapify_down(self, i): min_index = i left = self.left_child(i) if left < len(self.heap) and self.heap[left] < self.heap[min_index]: min_index = left right = self.right_child(i) if right < len(self.heap) and self.heap[right] < self.heap[min_index]: min_index = right if i != min_index: self.heap[i], self.heap[min_index] = self.heap[min_index], self.heap[i] self._heapify_down(min_index)3. 最小-最大堆
最小-最大堆的性质是:树中偶数层的每个节点都小于它的所有后代,而树中奇数层的每个节点都大于它的所有后代。
用途 双端优先级队列
class MinMaxHeap: def __init__(self): self.heap = [] def parent(self, i): return (i - 1) // 2 def left_child(self, i): return 2 * i + 1 def right_child(self, i): return 2 * i + 2 def get_min(self): if not self.heap: return None return self.heap[0] def get_max(self): if not self.heap: return None if len(self.heap) == 1: return self.heap[0] if len(self.heap) == 2: return self.heap[1] if self.heap[1] > self.heap[0] else self.heap[0] return self.heap[1] if self.heap[1] > self.heap[2] else self.heap[2] def insert(self, item): self.heap.append(item) self._heapify_up(len(self.heap) - 1) def extract_min(self): if not self.heap: return None min_item = self.heap[0] last_item = self.heap.pop() if self.heap: self.heap[0] = last_item self._heapify_down_min(0) return min_item def extract_max(self): if not self.heap: return None max_item = self.get_max() max_index = self.heap.index(max_item) self.heap[max_index] = self.heap[-1] self.heap.pop() if max_index < len(self.heap): self._heapify_down_max(max_index) return max_item def _heapify_up(self, i): if i == 0: return parent = self.parent(i) if self.heap[i] < self.heap[parent]: self.heap[i], self.heap[parent] = self.heap[parent], self.heap[i] self._heapify_up_max(parent) else: self._heapify_up_min(i) def _heapify_up_min(self, i): grandparent = self.parent(self.parent(i)) if i > 2 and self.heap[i] < self.heap[grandparent]: self.heap[i], self.heap[grandparent] = self.heap[grandparent], self.heap[i] self._heapify_up_min(grandparent) def _heapify_up_max(self, i): grandparent = self.parent(self.parent(i)) if i > 2 and self.heap[i] > self.heap[grandparent]: self.heap[i], self.heap[grandparent] = self.heap[grandparent], self.heap[i] self._heapify_up_max(grandparent) def _heapify_down_min(self, i): while True: min_index = i left = self.left_child(i) if left < len(self.heap) and self.heap[left] < self.heap[min_index]: min_index = left right = self.right_child(i) if right < len(self.heap) and self.heap[right] < self.heap[min_index]: min_index = right if i != min_index: self.heap[i], self.heap[min_index] = self.heap[min_index], self.heap[i] i = min_index else: break def _heapify_down_max(self, i): while True: max_index = i left = self.left_child(i) if left < len(self.heap) and self.heap[left] > self.heap[max_index]: max_index = left right = self.right_child(i) if right < len(self.heap) and self.heap[right] > self.heap[max_index]: max_index = right if i != max_index: self.heap[i], self.heap[max_index] = self.heap[max_index], self.heap[i] i = max_index else: break在这个实现中,MinMaxHeap类代表一个min-max堆,包含一个list堆,用于存放堆中的元素。 parent、left_child 和right_child 方法分别返回节点的父节点、左子节点和右子节点的索引。 get_min 方法返回堆中的最小元素,get_max 方法返回堆中的最大元素。 insert 方法将一个元素插入到堆中并维护堆属性。 extract_min 方法从堆中移除最小元素并保持堆属性。 extract_max 方法从堆中移除最大元素并保持堆属性。
_heapify_up、_heapify_up_min、_heapify_up_max、_heapify_down_min 和 _heapify_down_max 方法用于维护最小-最大堆属性。 _heapify_up 在向堆中插入元素后调用,以确保元素位于正确的位置。 _heapify_up_min 和 _heapify_up_max 由 _heapify_up 调用以维护最小-最大堆属性。 _heapify_down_min 和 _heapify_down_max 分别被 extract_min 和 extract_max 调用,以维护 min-max 堆属性。
标签:
python实现堆(最大堆、最小堆、最小最大堆) 当前观察
最小-最大堆的性质是:树中偶数层的每个节点都小于它的所有后代,而树中奇数层的每个节点都大于它的所有后代。
2023-04-03昆明提高“两病”用药保障水平_全球速读
记者从有关方面获悉,4月1日起,昆明市启动实施进一步提高昆明市医保参保人“两病”(高血压和糖尿病)用药保障水平新政策,全
2023-04-03天天微资讯!年报速递|世茂服务去年收入约86亿元,毛利超19亿元
3月31日,世茂服务控股有限公司(简称“世茂服务”)发布2022年度业绩公告。公告显示,2022年,世茂服务实现收入约86 37亿元,同比增长3 5%。在
2023-04-032023第二季度天津河北区公租房摇号顺序是什么?-全球播报
》》》2023第二季度天津河北区公租房摇号顺序是什么?答:按照优先组家庭、租房补贴其他组家庭和非租房补贴其他组家庭分组顺序依次进行摇号。
2023-04-03车子被追尾怎么处理?
汽车发生追尾后,处理方法可以按照如下进行:1、车辆驾驶人应当立即停车,保护现场。2、持续开启危险报警闪光灯,并在来车方向设置警告标志等
2023-04-03焦点资讯:嘴哥回归在即?维金斯老婆晒动态:湾区有啥好Tony老师推荐吗?
维金斯老婆今日更新Instagram动态。维金斯老婆晒出了自拍,并询问湾区有没有卷发专攻的好Tony老师。维金斯老婆的Instagram定位也已经定位到了湾区
2023-04-03
x
广告

苏炳添、谢震业入围尤金世锦赛参赛资格 巩立姣冲击3连冠
2022-07-10
未来3个月 U21国足将与克罗地亚乙级队进行热身
2022-07-10
行走河南·读懂中国|2022年文化和自然遗产日河南主场活动进行
2022-07-05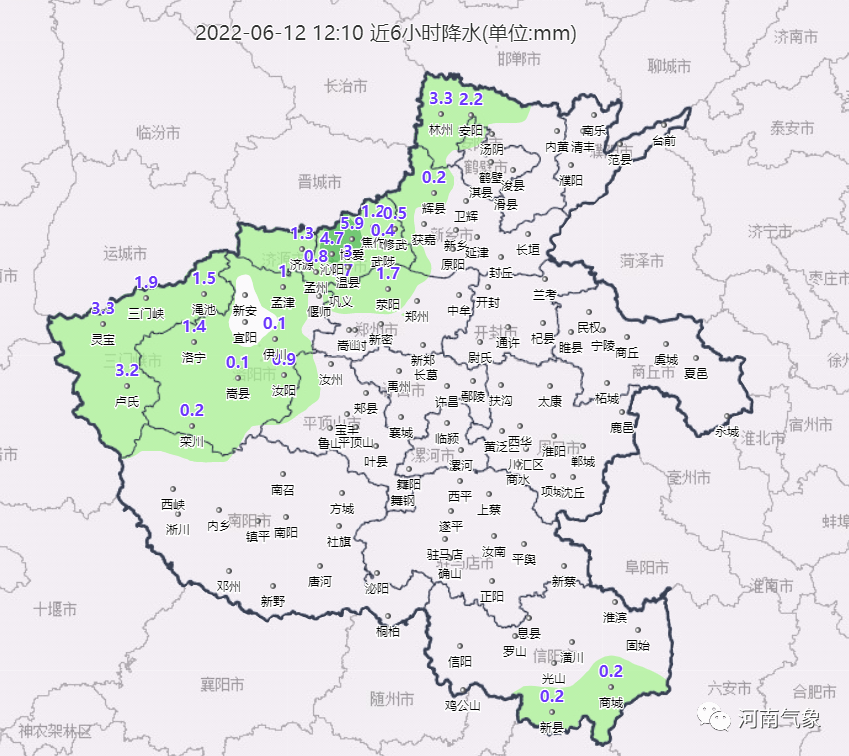
未来三天河南强对流天气出没频繁 注意防范
2022-07-05四川出台措施推动工业经济上行 聚焦中小微企业纾困帮扶等方面
月13日,记者从四川省经济和信息化厅获悉,为认真落实党中央、国务院和省委、省政府关于稳住经济大盘系列政策措施,奋力推动工业经济尽快回
2022-09-15楼阳生:做强“空中丝路” 做大枢纽经济
6月14日,省委书记楼阳生为河南民航发展投资集团有限公司揭牌。 记者 董亮 蔡迅翔 摄6月14日,河南民航发展投资集团有限公司揭牌暨航空
2022-07-05河南:十二条土地新政策助力稳经济促增长
记者从6月14日召开的全省自然资源系统服务保障稳经济保增长工作视频会议上获悉,经省政府同意,省自然资源厅出台12条稳经济促增长规划用地
2022-07-05河南最新物流行业纾困措施来了 多税种减半征收
为给河南省常态化疫情防控下的货运保障工作再上一道保险栓,6月14日,河南省公布了《支持物流行业纾困解难若干政策措施》(下文简称《措施
2022-07-05
x
广告
